贝叶斯滤波学习笔记

贝叶斯滤波可以用于去除观测信息中的噪音。

贝叶斯学派

贝叶斯理论将人们的主观经验称为先验概率，在主观经验的基础上的到某个结果的概率叫做似然概率，而将那个结果作用于先验信息，最终更新先验概率得到的预测结果的概率叫做后验概率。

贝叶斯定理的公式：

\begin{aligned} P(H|E)=&\frac{P(HE)}{P(E)}=\frac{P(H)P(E|H)}{p(E)}\\ =&\frac{P(H)P(E|H)}{\sum P(H_i)P(E|H_i)}=\eta P(H)P(E|H) \end{aligned}

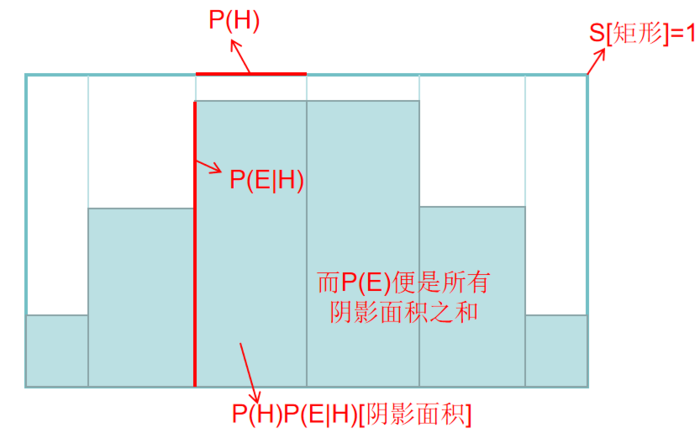
其中 $P(H)$ 为先验概率， $P(E|H)$ 为似然概率。

举一个实际例子：

比如此时想要测量气温，根据经验我们有以下先验概率，记为 $P(T$ )：

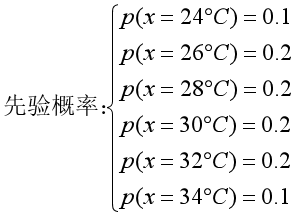
那么假设温度计显示的是29度，我们分析今天气温是30度的概率。

$P(T=30)$ ：先验概率，即今天是30读的概率。对应 $P(H)$ 。

$P(T_m=29|T=30)$ ：似然概率，即今天气温是30度条件下温度计是29度的概率。对应 $P(E|H)$ 。

$P(T_m=29)$ ：所有可能的温度下温度计时29度的概率之和。对应 $P(E)$ 。

$P(T=30|T_m=29)$ ：后验概率，即温度计是29度条件下今天气温是30度的概率。对应 $P(H|E)$ 。

P(T=30|T_m=29)=\frac{P(T_m=29|T=30)P(T=30)}{P(T=30)}

将离散的形式拓展到连续：

将概率化为一个具体的区间，先求 $P(X<x|Y=y)$ ，并转换为求和，则有：

P(X<x|Y=y)=\sum_{u=-\infty}P(X=u|Y=y)=\sum_{u\to-\infty}^{x}\frac{P(Y=y|X=u)P(X=u)}{P(X=y)}

将概率转换为一个极小的区间：

P(X<x|Y=y)=\lim_{\varepsilon\to0}\sum^x_{u=-\infty}\frac{P(y<Y<y+\varepsilon|X=u)P(u<X<u+\varepsilon)}{P(y<Y<y+\varepsilon)}

将小区间下的概率转换为密度函数在小区间上的积分：

P(X<x|Y=y)=\lim_{u\to-\infty}\sum_{u=-\infty}^x\frac{\int_y^{y+\varepsilon}f_{Y|X}(y|u)\mathrm{d}y\int_u^{u+\varepsilon}f_X(u)\mathrm{d}u}{\int_y^{y+\varepsilon}f_Y(y)\mathrm{d}y}

其中 $f$ 为概率密度函数。

再运用中值定理：

P(X<x|Y=y)=\lim_{\varepsilon\to0}\sum_{u=-\infty}^x\frac{[f_{Y|X}(\xi_1|u)\varepsilon][f_X(\xi_2)\varepsilon]}{f_Y(\xi_3)\varepsilon}

其中：

\xi_1\in(y,y+\varepsilon)\\ \xi_2\in(u,u+\varepsilon)\\ \xi_3\in(y,y+\varepsilon)

易知：

P(X<x|Y=y)=\lim_{\varepsilon\to0}\sum_{u=-\infty}^x\frac{f_{Y|X}(y|x)f_X(x)}{f_Y(y)}

转换为积分形式：

P(X<x_0|Y=y)=\int_{-\infty}^{x_0}\frac{f_{y|x}f_X{x}}{f_Y(y)}=\int_{-\infty}^{x_0}f_{X|Y}(x|y)\mathrm{d}x

两边消去积分，得到连续随机变量下的贝叶斯公式：

f_{X|Y}(x|y)=\frac{f_{Y|X}(y|x)f_X(x)}{f_Y(y)}

贝叶斯滤波（及衍生出的卡尔曼、粒子）基本思想：对观测和预测的数据做加权平均。

概率是怎么得来的？

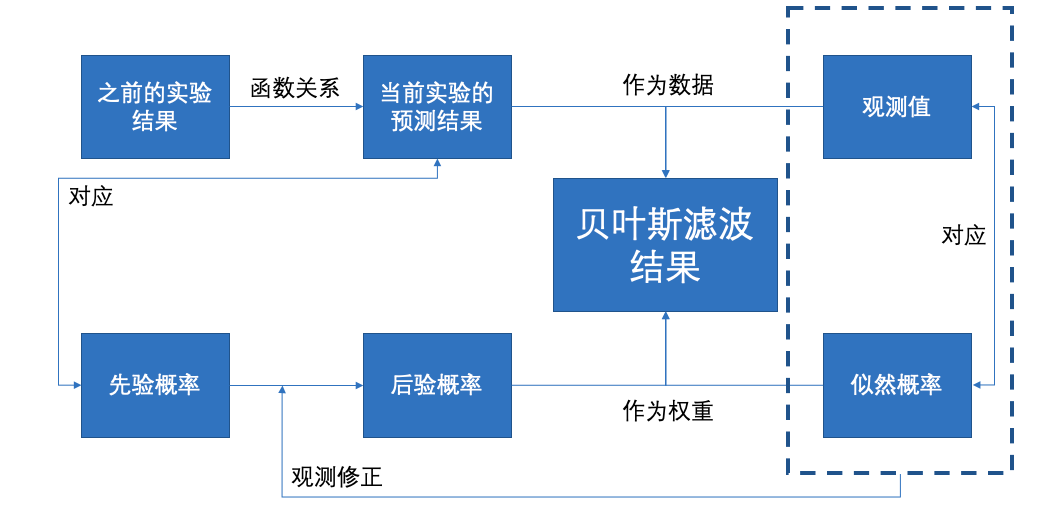
随着实验的外部观测修正最初的概率值，最终逼近实验概率的真实值。

先验概率->（观测）后验概率

对于每一次实验，贝叶斯理论取消了独立性的概念，因此每一次实验的变量都是相关的，即：

x_k=f(x_{k-1})

并且每一次实验的概率也相关，即：

P(x_k)=F(P(x_{k-1}))

$x_k$ 预测值， $P(x_k)$ 先验概率

优点：完美解决了多传感器的数据融合和滤波问题

缺点：无穷积分电脑做不出来

改进：

卡尔曼滤波：把随机变量间的关系函数f限定为线性函数 $X_k=AX_{k-1}+B$

粒子滤波：用蒙特卡洛积分法近似计算非线性函数 $f$