感知机模型和其相关算法笔记。
感知机
- 输入空间: X⊆Rn ;输入:x=(x1,x2,...,xn)T∈X
- 输出空间: Y={+1,−1} ;输出 y∈Y
- 感知机:
f(x)=sign(w⋅x+b)={+1, w⋅x+b≥0−1, w⋅x+b<0
其中, w 称为权值(Weight), b 称为偏置(Bias), w⋅x 表示内积。
- 假设空间: F={f∣f(x)=w⋅x+b}
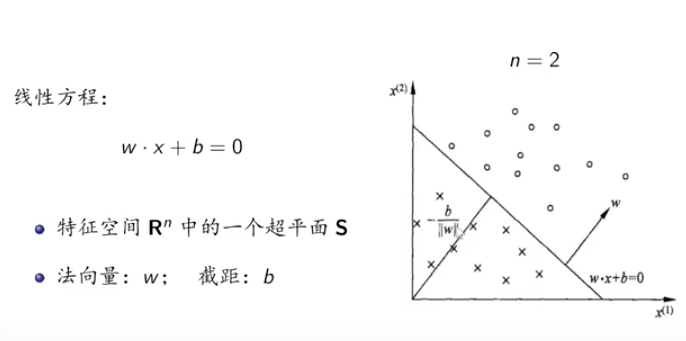
线性方程:
w⋅x+b=0
法向量: w,截距: b 。
区分正负的是特征空间 Rn 中的一个超平面 S 。这个超平面是 n−1 维的。
例如:当n=3时,可以利用2维的平面将三维空间划分为两个部分。我们可以感性地理解更高维的情况。
学习策略
要求:数据集线性可分
对于给定的数据集 T={(x1,y1),(x2,y2),...,(xN,yn)}
若存在某个超平面 S
w⋅x+b=0
能够将数据集的正负实例点完全正确的划分到超平面两侧,即
{yi=+1yi=−1w⋅xi+b>0w⋅xi+b<0
那么称数据集线性可分,否则不可分。
定义感知机的损失函数
定义 ∀x0∈Rn 到 S 的距离:
∣∣w∣∣1∣w⋅x0+b∣
若 x0 是正确分类点:
∣∣w∣∣1∣w⋅x0+b∣={∣∣w∣∣w⋅x0+b−∣∣w∣∣w⋅x0+by0=+1y0=−1
若 x0 是错误分类点:
∣∣w∣∣1∣w⋅x0+b∣={−∣∣w∣∣w⋅x0+b∣∣w∣∣w⋅x0+by0=+1y0=−1=∣∣w∣∣−y0∣w⋅x0+b∣
误分类点 xi 到 S 的距离:
−∣∣w∣∣−yi∣w⋅xi+b∣
所有误分类点到 S 的距离:
−∣∣w∣∣1∑yi∣w⋅xi+b∣
系数 −∣∣w∣∣1 不影响算法。终止点是 S=0 。
梯度下降法
求解无约束最优化问题。
梯度:指某一函数在该点处最大的方向导数,沿着该方向可以取得最大的变化率。
∇=∂θ∂f(θ)
若 f(θ) 为凸函数,则可以通过梯度下降法进行优化取得最小值:
θ(k+1)=θ(k)−η∇f(θ(k))
其中 η 指步长。
算法
输入:目标函数 f(θ) ,步长 η ,精度 ϵ 。
输出: f(θ) 的极小值点
- 选取初始值 θ(0)∈Rn ,置 k=0 。
- 计算 f(θ(k) 。
- 计算梯度 ∇f(θ(k)) 。
- 置 θ(k+1)=θ(k)−η∇f(θ(k)) ,计算 f(x(k+1)) ,当 ∣∣f(θ(k+1)−f(θ(k)))∣∣<ϵ 或者 ∣∣θ(k+1)−θ(k)∣∣<ϵ 时停止迭代 θ∗=θ(k+1) 。
- 否则 k=k+1 ,继续第3步
计算梯度:
-
单变量
f(x) 那么 ∇x=∂x∂f=dxdf 。
-
多变量
F(Θ)=5θ12+2θ2+θ34,Θ=(θ1,θ2,θ3)T
分别对三个变量求偏导。
∇θ1=∂θ1∂F(Θ)=10θ1∇θ2=∂θ2∂F(Θ)=2∇θ3=∂θ3∂F(Θ)=4θ3
得出
∇Θ=(10θ1,2,4θ33)T
一个例子:

原始形式算法
训练数据集: T={(x1,y1),(x2,y2),...,(xN,yn)} 其中,xi∈X⊆Rn,yi∈{+1,−1}
损失函数: L(w,b)=−∑xi∈Myi(w⋅xi+b) ,其中, M 表示所有误分类点的集合。
模型参数估计:
argw,bminL(w,b)

批量梯度下降需要大量计算。随机梯度下降计算更简便。
算法的收敛性
计 w^=(wT,b)t , x^=(xT,1)T ,则分离超平面可以写为 w^⋅x^=0 。

- 收敛性:对于线性可分的 T ,经过有限次的搜索,可得到将 T 完全分离开的超平面。
- 依赖性:分离超平面的结果依赖于不同的初值选择,或者迭代过程中不同的误分类点的选择顺序。
- 对于线性不可分的 T ,迭代结果会发生震荡,无法收敛。
- 为得到唯一的分离超平面,需增加约束条件。
对偶形式的学习算法
在原始形式中,若 (xi,yi) 为误分类点,可如下更新参数:
w←w+ηyixib←b+ηyi
假设初始值 w0=0,b0=0 ,对误分类点 (xi,yi) 通过上述的公式更新参数,修改 ni 次后, w,b 的增量分别是 αiyixi 和 αiyi ,其中 αi=niηi 。
最后学习到的参数为:
w=i=1∑Nαiyixib=i=1∑Nαiyi





