The Components of a Formal System

• Axioms: The basic assumptions that are taken for granted.
• Inference Rules: The rules that allow us to derive new theorems from the axioms.
• Theorems: The statements that can be derived from the axioms using the inference rules.
• Proofs: The process of deriving theorems from the axioms using the inference rules.
• Consistency: A formal system is consistent if it is impossible to derive a contradiction from the axioms.
• Completeness: A formal system is complete if every true statement can be proven within the system.
• Decidability: A formal system is decidable if there is an algorithm that can determine whether a given statement is a theorem of the system.

Take the MU-puzzle for an example.

• Axioms: MI
• Inference Rules:
  1. If a theorem whose last letter is $I$, then you can add a $U$ to the end.
  2. If $Mx$ is a theorem, then $Mxx$ is a theorem.
  3. If $III$ appears in a theorem, then it can be replaced by $U$.
  4. If $UU$ appears in a theorem, then it can be deleted.
• Proofs: Prove that $MIIU$ is a theorem.
  • $MII$ (from $MI$ using the first inference rule)
  • $MIIII$ (from $MII$ using the second inference rule)
  • $MIIU$ (from $MIIII$ using the third inference rule)

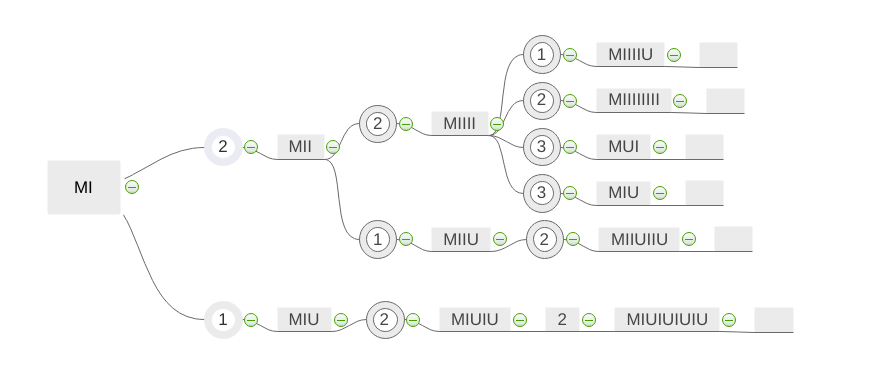
It’s noticable that the Chinese version of MU-puzzle uses “WJU” three letters instead of “MIU”. I will explain the reason in the later section.

Is $MU$ a theorem?

It’s obvious that all the theorems in the MU-puzzle are of the form $Mx$, where $x$ is a string of $I$ and $U$. The reson is, none of the reference rules can add an $M$ to the theorem or remove $M$.

This conclusion is based on the observation of the structure of the theorems in the MU-puzzle. We call this kind of reasoning is jumping out of the system.

However, we still can not determine whether $MU$ is a theorem or not. We can try to list all the theorems in the MU-puzzle and check if $MU$ is in the list. But this is not a feasible solution because the number of theorems grows exponentially with the length of the string. In a more technical term, we can not determine whether $MU$ is a theorem in a finite amount of time.

Bottom-up and Top-down

Bottom-up: Start from the axioms and use the inference rules to derive the theorems.

Top-down: Start from the theorems and try to find the axioms that can derive them.

The previous section is an example of the bottom-up approach. The top-down approach is more difficult.

We use $pq$ formal system to illustrate the top-down approach. The axioms of the $pq$ formal system are:

• Axioms: $x-qxp-$, where $x$ is any string of $-$.
• Inference Rules: If $xqypz$ is a theorem, then $x-qypz-$ is a theorem.

The only inference rule shows that when the $x$ plus one then $z$ must also plus one.

It’s easy to see that the theorems of the $pq$ formal system are of the form $xqypz$, and must meet $x=y+z$.

So when we want to decide whether a string is a theorem of the $pq$ formal system, we can simply just check if the number of the hypens meet the requirement of the theorem.

For example, $----q--p--$ is a theorem of the $pq$ formal system because $4=2+2$.

This kind of reasoning is called the top-down approach.

M-Mode, I-Mode, and U-Mode

The MU-puzzle was stated in such a way that it encouraged some amount of exploration whthin the MIU-system-deriving theorems. But it was also stated in a way so as not to imply that staying inside the system would necessarily yield fruit.

There are three thinking modes in the MU-puzzle:

• Mechanic-Mode: The mode in which you are following the rules of the system mechanically. You simply write down all the theorems that you can derive from the axioms using the inference rules one by one.
• Intelligent-Mode: The mode in which you are trying to understand the structure of the theorems in the system. You are trying to see if there is a pattern or a rule that governs the theorems.
• Un-Mode: A Zen way of approaching the problem.

This is why the Chinese version of the MU-puzzle uses “WJU” three letters instead of “MIU”. The “W” stands for “惟” which means “from your heart” in Chinese, “J” stands for “机” which means “mechanic”, and “U” stands for “无” which means “nothing”.

Isomorphism Induce Meaning

We have created two formal systems “WIU” and “pq” system, however, there is no obvious “meaning” of the two systems.

We need to create a kind of mapping between the formal system and the real world to give the system meaning. This is called isomorphism.

For example, the “pq” system can be mapped to the addition of two numbers.

$$\begin{aligned} q &\iff =\\ p &\iff +\\ - &\iff 1\\ -- &\iff 2\\ --- &\iff 3\\ &\vdots \end{aligned}$$

The isoformism is not unique. We can also map the “pq” system to the minus of two numbers.

The Misbehaviour of Arithmetic

The pq-system gives us a way to represent the addition of two numbers. Let’s think more about the number system.

People enjoy inventing slogans which violate basic arithmetic but which illustrate “deeper” truths, such as “1+1=1 (for lovers)”, or “1+1+1=1 (the Trinity)” … Two raindrops running down a windowpane merge; A cloud breaks up into two clouds.If you think about the quesion, you will probably come up with some criterion involving separation of the objects in space, and making sure each one is clearly sidtinguishable from all the others.

Numbers as realites misbehave. However, there is an ancient and innate sense in people that numbers ought not to misbehave.

Liberation, by M.C. Escher

One misbehaviour of numbers could be the infinite series. Take the example the Euclid’s theorem, which states that there are infinitely many prime numbers.

The proof of the theorem is to tell people, no matter how big the number you pich, there is always a bigger prime number. Let’s pick the number $N$. We can construct a new number $N!+1$. And this new number can not be divided by any number from $2$ to $N$. In another word, $N!+1$ can only possibly be divided by a number bigger than $N$. So either it is itself prime or prime disvisors are greater than $N$.

The way we get around infinite is to use the concept of “potential infinity”. We use the statement “all” in a few ways which are defined by the thought processs of reasoning.

Sonata for Unaccompanied Achilles

This is a veeery interesting story.

Douglas presents an isoformism word puzzle.

A word with the letters ‘A’, ‘D’, ‘A’, ‘C’ consecutively.

A word that begins with letters “HE” and also ends with “HE”.

The answer is headache.

The Chinese version of the puzzle is also ingenious.

一个词语，其中两个部首依次是“昔”和“火” (A word with the two radicals “昔” and “火” consecutively.)

一个词语，以部首“虫”开头，以部首“虫”结尾 (A word that begins with the radical “虫” and also ends with “虫”.)

The answer is “蜡烛” which means candle.