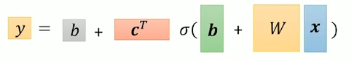宏观理解机器学习和深度学习。
机器学习
寻找一个函数
eg:语音识别 声音->文字
机器学习的任务
回归(Regression):函数输出为数值
分类(Classification):给定一些选项,函数输出为正确的选项
结构化学习(Structured Learning):获得有结构的物体
机器学习的步骤
-
找一个带未知参数的函数(Function with unkown)
也被称作模型eg: y=b+wx1 ,其中 w,b 为未知参数
-
从训练数据中定义Loss(Define loss from training data)
Loss是关于未知参数的函数 L(w,b) ,用来衡量未知参数好不好
真实的值称为Label,预测值与真实值的差即为计算误差
累计差距的方式有很多种:MAE(绝对值误差),MSE(均方误差)
误差等高线图(Error Surface)
-
优化(Optimization)
w∗,b∗=argminw,bL
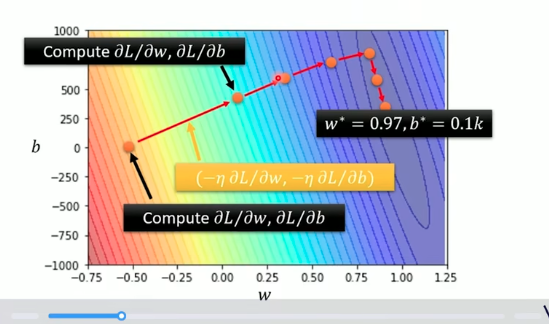
梯度下降(Gradient Descent):
先假设未知参数只有 w 。先随机取定一个 w0(利用遗传算法)。
计算 L 对 w0 的偏导( w0 在误差曲线上的切线斜率)
w1=w0−η∂w∂L∣w=w0
η 被称为学习速率(learning rate)。
这种机器学习中需要自己设定的东西称为超参数(hyperparameters)
反复进行上述的操作。
停止:达到最大迭代速率或找到某一极值(Local minima),无法保证一定找到全局最优解。
当有多个参数时。先随机取定 w0,b0。
计算 L 对 w0 和 b0 的偏导。
w1=w0−η∂w∂L∣w=w0,b=b0b1=b0−η∂b∂L∣w=w0,b=b0
反复更新 w,b 。
y=b+j=1∑7wjxj
被称为线性模型
分段线性折线(常数+一系列折线)
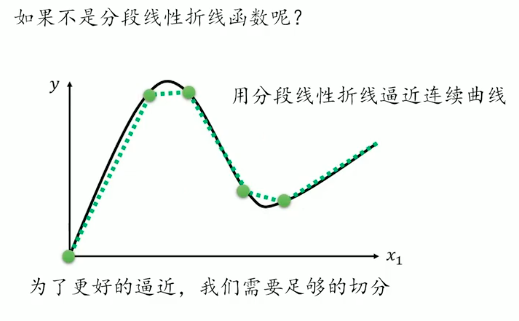
- 找一个带未知参数的函数,我们用Sigmoid函数来表示这类折线
y=c1+e−(b+wx1)1=c sigmoid(b+wx1)
w——斜坡的坡度
b——相位
c——高度
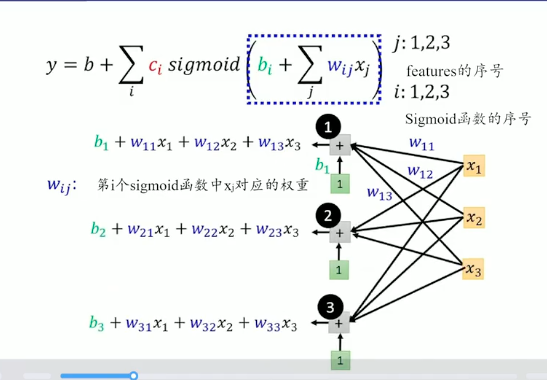
y=b+i∑cisigmoid(bij∑wijxj)
wij 表示的是第 i 个函数中 xj 对应的权重。

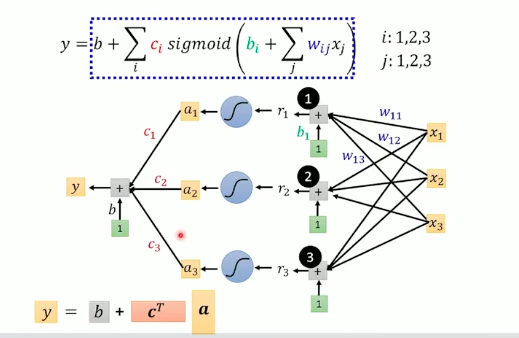
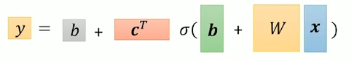
- 定义Loss
e=∣y−y^∣Loss:L=N1n∑en
-
优化

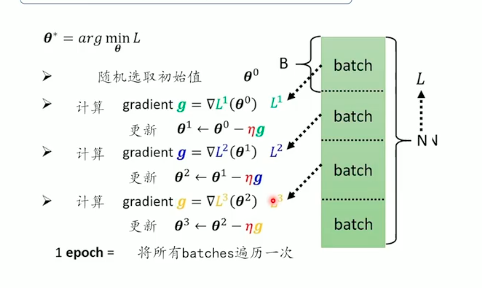
ReLU模型:
y=b+2i∑cimax(0,bi+j∑wijxj)
称为激活函数。激活函数的部分称为神经元,很多神经元组成这个模型,叫做神经网络。很多隐藏层就形成了深度学习。